The Extraordinary Properties of Artificial Metamaterials

Understanding how a class of manmade materials can seemingly defy the laws of physics

Sep 08, 2024

In 1968, Victor Veselago discovered something remarkable.

He hypothesized a new class of materials with extraordinary properties that seemingly defy laws of physics. There was one small problem. These materials do not naturally occur in our known universe.

Luckily for us, we have found ways to engineer them, at least to some extent.

In this article, we will explore the amazing properties of metamaterials. We will cover:

The existence of ether
Wave propagation in materials
The amazing properties of metamaterials
Making metamaterials at microwave frequencies

Read time: 10 mins

To Ether or not to Ether?

Let me tell you a story.

Scientists in the nineteenth century believed that there should be an unseen "elastic, compressible, non gravitational solid" known as luminiferous (meaning light-bearing) ether that is widespread in our cosmos and allows electromagnetic waves to propagate. The concept of an invisible medium makes sense when you consider a rock thrown into motionless water. Waves can be seen spreading outward from the point of impact. Even sound waves go through air vibrations. A considerable part of the last century was focused on studying "ether mechanics" and the most renowned proponent of the notion was William Thomson/Lord Kelvin, who dedicated his entire life to the qualities of ether. He wrote:

Ether of Space has been my life study. ... I always meant some day to write a scientific treatise about the Ether of Space; but when in my old age I came to write this book, I found that the Ether pervaded all my ideas, both of this world and the next. I could no longer keep my treatise within the proposed scientific confines; it escaped in every direction and now I find has grown into a comprehensive statement of my philosophy.

In 1887, scientists Albert Michelson and Edward Morley conducted an experiment to detect the presence of ether. They created a mechanism that divided a light beam in two, rebounded it off a mirror, and targeted it at a detector. If ether existed, the speed of light would vary depending on whether it was moving in the same direction as the earth's motion or at right angles. They expected the light beams to arrive at the detector at different times. To their dismay, the beams of light arrived at the same time, demonstrating that ether did not exist.

In 1905, the annus mirabilis "miracle year," in the paper titled On the Electrodynamics of Moving Bodies, Albert Einstein wrote:

The introduction of a “luminiferous ether” will prove to be superfluous inasmuch as the view here to be developed will not require an “absolutely stationary space” provided with special properties...

He was suggesting that describing electromagnetic phenomena did not necessitate the use of ether. He did not argue ether does not exist; he simply stated that it is not required to explain physical phenomena.

Except for Germany, Einstein's study on relativity received little attention. The widely established concept of ether represented the status quo, and most physicists dismissed Einstein's theory as impracticable and nonsensical.

Einstein returned to the concept of ether in 1920 in an attempt to incorporate gravity into special relativity. Without the concept of ether, he discovered that gravity's "action-at-a-distance" was mechanically inconsistent. In 1693, Newton saw the need for a "medium" in which gravity could function, and that gravity's ability to generate mechanical movement through vacuum was a ludicrous idea. He wrote:

That gravity should be innate, inherent, and essential to matter, so that one body may act upon another at a distance through a vacuum, without the mediation of anything else, and by and through which their action and force may be conveyed from one to another, is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it.

Today's widely accepted view is that ether does not exist, the propagation of electromagnetic waves can occur in free space, and that gravity does indeed occur at a distance. While waves can propagate in a material medium, it is not required to be present for waves to travel.

Despite this understanding, we "confusingly" assign constitutive parameters such as permittivity and permeability to a vacuum. How can we assign material parameters if there is no material present? There is an explanation. According to quantum field theory, vacuum gets polarized due to fleeting formations of electron-positron pairs, and thus assigning permittivity to a vacuum is actually possible.

Wave Propagation in Materials

Wave propagation in a physical medium is simpler to visualize. Permittivity and permeability are macroscopic properties of a substance that govern how waves propagate through it. It is macroscopic in the sense that the fundamental units (atoms, molecules, or something manmade) are much closer together than the wavelength of the wave passing through it.

Permittivity indicates how the medium responds to an external electric field. When an electric field is produced, the ease with which the dipoles in the medium line up with the field is a measure of its permittivity, which is often symbolized by the greek letter ε (epsilon). In vacuum, ε0=8.854 x 10^-12 Farad/meter. A material's permittivity is typically given as a multiple of ε0, depicted by εr, or relative permittivity. For example, glass has a relative permittivity of ~4, or four times that of vacuum.

Permeability describes the medium's response to an external magnetic field and is a measure of the amount of magnetism induced in a substance. It is designated by the Greek letter μ (mu), and μ0 = 4π x 10^-7 Henry/meter in vacuum. μr expresses a material's permeability as a multiple of that of vacuum. For example, carbon steel has a permeability of approximately 100.

The refractive index of a substance is the square root of the product of its relative permittivity and permeability. The +/- sign in front is preserved because, as we will see, negative refractive index materials can be manufactured to have extraordinary qualities.

The figure below shows the possible space of values for permittivity and permeability.

Positive values of permittivity and permeability encompasses most naturally occurring dielectric materials (upper right quadrant I)
Plasma and doped semiconductors at certain frequencies exhibit negative permittivity and positive permeability (upper left quadrant II)
Some ferrites especially at low frequencies show negative permeability but positive permittivity (lower right quadrant IV)
No known naturally occurring materials exist with both negative permittivity and permeability (lower left quadrant III)

The Amazing Properties of Double Negative Materials

In 1968, Victor Veselago, a Soviet Russian physicist investigated this lower left quadrant and published a theoretical analysis of the properties of these "unnatural" materials with both negative permittivity and permeability, known as double negative materials in more recent literature. Veselago explored what would happen to wave propagation in this hypothetical medium, supposing it existed. What he discovered was extraordinary.

Left-handed Materials

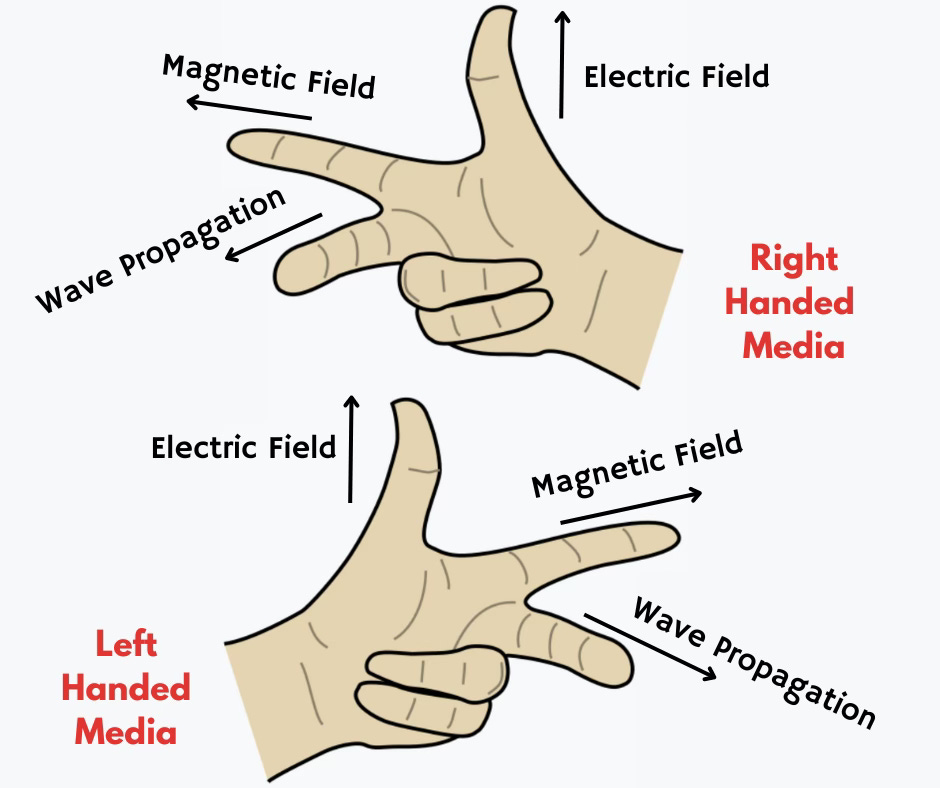
Veselago began by examining situations where ε and μ occur individually, such as in Maxwell's equations. Maxwell's equations, when solved in regular materials with positive ε and μ, determines the direction of wave propagation using the right hand rule.

Make a mutual right angle with your thumb, index, and middle fingers. If the electric field is pointing in the direction of the thumb and the magnetic field is pointing in the direction of the index finger, the middle finger indicates the direction of wave propagation.

Thumb image credit: https://commons.wikimedia.org/wiki/File:Right_hand_rule_cross_product.svg

If both ε and μ are negative, wave propagation in these materials follows the left hand rule, where each finger represents the same quantity. If you try it out, you'll notice that the direction of wave propagation is backwards compared to materials with positive constitutive parameters. Naturally, these materials came to be called "left handed metamaterials."

Reversal of Physical Phenomena

Reversing the signs of ε and μ reverses several physical phenomena. This is remarkable considering that anything in nature can be made to work backwards relative to how they usually function.

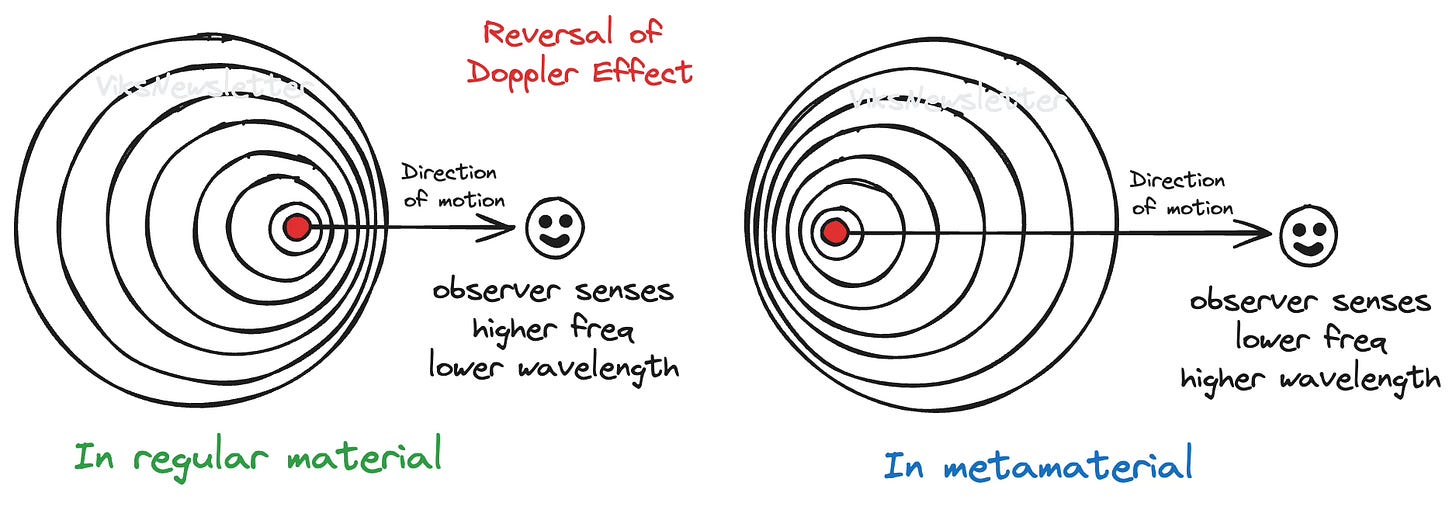
Doppler Effect

The phenomena of backward wave propagation indicates that the doppler effect will be reversed. A receding train siren would move to higher frequencies rather than lower ones. If vacuum was a left-handed medium, the red shift from an expanding galaxy would be blue. Scientists have demonstrated the reversal of the doppler effect by shining a CO2 laser through an array of tightly spaced silicon rods, which serve as a left handed metamaterial.

Vavilov-Cherenkov Effect

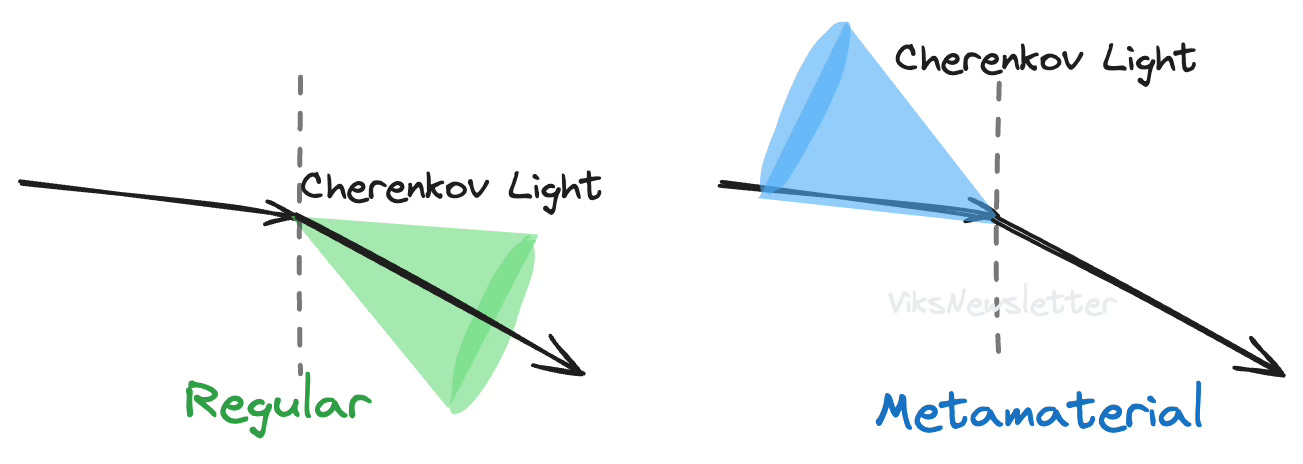
Cherenkov effect is the emission of radiation when a charged particle travels in a dielectric medium with a phase velocity faster than that of light. Think of it like a sonic boom, but a photonic shock-wave for charged particles exceeding speed of light. This is actually what makes underwater nuclear reactors emit blue light.

In a right-handed medium, the emission of Cherenkov radiation occurs in the forward direction of the wavefront. In left-handed materials, the radiation occurs in the reverse direction — behind the wavefront of the moving particle.

Researchers have demonstrated the reversal of Cherenkov radiation at microwave frequencies by pushing charged particles through slot waveguides. Reversed Cherenkov radiation has many possible applications in electronic devices, particle detectors, and accelerators.

Snell's Law

Snell's law determines the angle of refraction when a ray of light goes from one medium to another with different refractive indices. If a ray of light traveling in a medium of refractive index n1 is incident at angle of θ1 at the interface of two materials, then the angle of propagation θ2 in a medium of refractive index n2 is given by

This equation is well understood when the media on both sides of the interface are right handed. But when one medium (say n2) has a negative refractive index, the angle of refraction θ2 is negative to satisfy Snell's law.

Negative angle of refraction creates some interesting optical phenomena. Usually, convex lenses converge light and concave lenses diverge light. If the lens were made of a double negative index metamaterial, it would do the opposite — convex lenses will be divergent and concave lenses will convergent. The formation of “super lenses” for perfect imaging is another possibility with metamaterials.

Making Double Negative Metamaterials

Victor Veselago received a Nobel Prize nomination in 2011 for his work on negative refraction in electrodynamics. However, after his first paper in 1968, his analysis went virtually overlooked for the next thirty years. Until, in 1996, Sir John Pendry from Imperial College, London, found a way to make materials with negative ε and μ.

Sir Pendry discovered that a cubic grid of very thin metallic wires exhibits negative ε at GHz frequency. Three years later, he proposed that two concentric "split-rings" dubbed a split ring resonator, when arranged in a lattice, exhibits negative μ. These findings were a big step forward in the development of artificial metamaterials.

A couple of years later, Prof. David Smith and his team from the University of California, San Diego, demonstrated that the thin metallic wires and split ring resonators could be combined to create a metamaterial with simultaneously negative ε and μ, and experimentally showed that negative index of refraction is possible at microwave frequencies. Implementing this at optical frequencies is significantly more difficult due to the nanoscale of the artificial structures involved, and it is still a subject of ongoing research.

Although Veselago mentioned it briefly in his original study, Sir Pendry demonstrated that a slab of double negative material can overcome the diffraction limitations imposed by normal lenses and function as a super lens. His discovery was so groundbreaking that he found it difficult to accept. As he says in an interview published in the journal Nature Light: Science and Applications:

I didn’t believe it. I thought, if I publish this, I’m going to be branded an idiot and my career will be finished in the optics. As you know, some people would have liked to see my career finished, so controversial was the result! But it wasn’t so. Eventually, we won through and persuaded people that this lens could do perfect focusing.

However, it has been hard to implement perfect lenses in practice and the era of super imaging resolution is still some ways off.

The applications of metamaterials are diverse, and encompasses electromagnetics, optics, acoustics, mechanics and elastics. Beyond super lenses, applications exist in metasurfaces, antennas, filters, frequency selective surfaces, absorbers, the list goes on.

It is a world of magic that is still an area of active research, and a topic we will keep revisiting in this newsletter.

If you like this post, please click ❤️ on Substack, subscribe to the publication, and tell someone if you like it. 🙏🏽

If you enjoyed this issue, reply to the email and let me know your thoughts, or leave a comment on this post.

Vik's Newsletter

Discussion about this post