Understanding Two Port Amplifier Power Gains
Transducer, Unilateral, Available and Power Gain; what they mean and how to calculate them.
I’m experimenting with different levels of technical content. Let me know what you think by replying to this email. Thanks! 🙏
If you find this helpful, share it with friends, colleagues or social media, and consider subscribing. It helps grow this newsletter!
Analog amplifiers can be usually defined in terms of voltage or current gain. In RF amplifiers, we deal with the concept of power gain which deals with both voltage and current at the same time. Due to high frequency signals being amplified, there is the issue of signal reflections at various interfaces in the amplifier circuit. Depending on which interfaces are chosen for input and output, you will have different definitions of power gain. This article explains what these definitions are.
In this article, you will learn the following:
Block-diagram representation of a two port amplifier
Impedances within the amplifier network
Power definitions at various amplifier interfaces
What the following power gains are:
Transducer gain
Unilateral gain
Power gain
Available gain
Utility in RF amplifier design
Let's dive in!
Two Port Amplifier Network
Fig 1 shows a simple two port amplifier. It has an active device for signal amplification and input/output matching networks. Matching networks are usually implemented with passive components. Their design depends on the impedance required at the active device terminals. For simplicity, we will consider these matching networks to be lossless.
The purpose of this network is to amplify an RF signal at its input to result in a stronger output signal. Gain is then the ratio of the output power to the power input to the network.
Impedance Definitions
Fig 2 shows all the impedance definitions in the two port amplifier needed for gain calculations.
Source and Load impedance
An input matching network transforms the generator impedance Z0 into an optimal value required at the active device input. The impedance looking into the input matching network towards the signal source is ZS. Its value significantly affects the gain and noise performance of the amplifier. Good amplifier design involves a careful choice of this impedance. From ZS, the source reflection coefficient is calculated as,
Similarly, the output matching network transforms the load impedance Z0 into an optimal value required at device output terminal. The impedance looking into the output matching network towards the load impedance is ZL. Proper choice of this impedance will dictate the linearity, efficiency, gain and output power at the amplifier load. Significant effort is usually dedicated to the optimal design of this impedance over a wide range of frequency. From ZL, the load reflection coefficient is given as,
Device Input and Output impedance
The impedance looking into the terminals of the active device is affected by both the s-parameters of the device itself and the matching network on the other side.
Input impedance Zin is affected by the device s-parameters and output matching network and its corresponding reflection coefficient is given by,
Output impedance Zout is affected by the device s-parameters and the input matching network and its corresponding reflection coefficient is given by,
In a "unilateral" device, there is no transfer of power from output to input. Then, S12=0. The input and output reflection coefficients reduce to S11 and S22 respectively. This is important for when we define "Unilateral Gain" later.
Power Definitions
Whenever there is an impedance mismatch between a matching network and an active device terminal, some of the RF power is transmitted and some is reflected. Maximum power transfer occurs when the source/load impedance is a complex conjugate of the device impedance. This is called conjugate matching.
When amplifiers have an arbitrary source/load impedance, there will be different power levels at different points in the two port amplifier network. Fig 3 shows all the power definitions in a two port amplifier. Understanding these will be key to defining various amplifier gains in the next section.
Power available from the source (Pavs): Maximum power that can be delivered to the active device from the source. This is only possible when the source impedance ZS is chosen to be the complex conjugate of input impedance Zin looking into the device.
Power delivered to the input (Pin): Power delivered to the input terminals of the active device. This does not make any assumptions about the input matching network. For any arbitrary ZS, there will be some reflected power back into the source, and the rest of the power delivered to the device is Pin. Pin is always less than or equal (under conjugate match) to Pavs.
Power available from the network (Pavn): Maximum power available from the output device terminal after amplification that can be delivered to the load. If the output impedance ZL is a complex conjugate of Zout, the impedance at the output of the device terminal, then this is the maximum power that can actually be delivered to the load.
Power delivered to the load (PL): Depending on the choice of output matching network and ZL, some power may be reflected back into the active device, and the rest of it is transmitted to the load. This is the actual power delivered to the load circuit. PL is always less than or equal (under conjugate match) to Pavn.
Transducer power gain
Transducer power gain (GT) is defined as
The ratio of the power delivered to the load to the power available from the source.
This is the most general and highly used definition of power gain in a two port amplifier. It makes no assumptions on the source and load impedances, or the behavior of the active device.
Fig 4 shows the reference planes and the formula to calculate the transducer power gain in a two port amplifier.
Even though there is no explicit dependence of the gain on S12, remember that it is included in the calculation of Γin from equation (3). The makes it a general definition of gain under all circumstances.
In the absence of matching networks, ZS = ZL = 50 Ω, or ΓS = ΓL = 0 (from equations (1) and (2)). In this case, the transducer power gain reduces to
This is the lowest possible gain you can obtain from the amplifier. Addition of any matching circuits will increase the power delivered to the active device and the load, hence increasing the gain.
Another useful approximation is to assume that S12=0. This is a reasonable assumption for many transistor devices whose reverse transmission is negligibly low. Under this condition, Γin = S11 and Γout = S22 (from equation 3, 4), which gives us a way to calculate the transducer power gain of an amplifier from only the s-parameters of the transistor and source/load reflection coefficients of the matching networks. This is called the unilateral transducer gain of the amplifier, given by equation 7(a).
It is simple to view unilateral transducer gain as a cascade of the gains of the source match (GS), intrinsic device (GT0) and load match (GL) networks.
To find the maximum unilateral transducer gain (GTUmax), the input and output needs to be conjugately matched, and by setting Γin = S11* and Γout = S22*, we get the maximum unilateral transducer gain as shown in equation 7(b).
Power Gain
Power gain (GP) is defined as
The ratio of the power delivered to the load to the power delivered to the input of the active device.
The gain definition will vary depending on the load matching network, but is independent of the source matching network because any reflections back into the source are already accounted for. In reality, the behavior of the active device depends on the source impedance presented to it, but we won't worry about it for now.
Fig 5 shows the reference planes used for calculation of power gain and the equation to do so.
Notice that this expression does not contain ΓS, making it independent of the source matching network. Power gain tells you how much power will be present at the load in the presence of a matching network when you provide a given power across the input terminals of the device.
If you need to calculate power gain with the source conjugately matched to the input, then it is as simple as setting Γin = S11*.
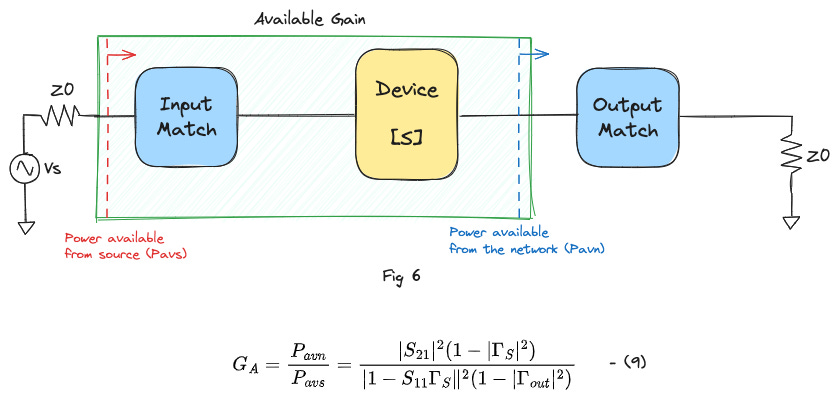
Available Gain
Available gain (GA) is defined as
The ratio between power available from network to the power available from the source.
Fig 6 shows the reference planes used in the calculation of available gain and the formula used to do so.
In contrast to power gain which was independent of the source matching network, available gain is independent of the load matching network, as shown in equation (9). Available gain tells you the maximum output power you can get from the device, when you provide all the power from the source to it.
If you need to calculate available gain with the load conjugately matched to the output, then set Γout = S22*.
Putting it together
All these gain definitions are tools to help you estimate if a given active device is:
suitable to meet the required gain specification for the amplifier
estimate how hard it is to get that performance
The first metric to look at while choosing an active device is maximum unilateral transducer gain (GTU,max) which makes the simplistic assumption that S12=0 and conjugate matching at both input and output. It gives you a sense of the power gain that is readily available from the device (assuming it is actually stable, but more on that in another article).
Designers rarely design for unilateral gain because the resulting amplifier is usually narrow band, sensitive to transistor s-parameters (especially S12) and it is hard to achieve stable performance at all frequencies.
By no means is GTU,max the absolute maximum gain possible from the device. With the proper kind of feedback, gain can even be infinite. When a device is pushed into oscillation, it produces output power with only noise power as its input. This results in gain values can exceed GTU,max.
Power gain can help estimate the designed gain while isolating only the load network, while being independent of the source network. Available gain allows you to do the same with the source network, while isolating the load network. They serve as intermediate gain estimates during the design process.
Transducer gain is the only gain that ultimately matters and represents the actual performance that is available from the amplifier in the presence of the actual, optimized source and load networks.
⭐️ Key Takeaways
There are several definitions of gain for a two port amplifier and understanding them is essential to RF amplifier design.
Transducer gain: This is the most realistic gain that can be reported for an amplifier that represents its actual performance in an RF system.
Maximum unilateral transducer gain: This is useful to understand what kind of gain is readily available from a device that has little feedback from output to input, and is conjugately matched (and stable).
Power and Available gain: These are useful to understand the amplifier gain by isolating the source and load networks, and are good for intermediate estimates during the amplifier design process.
Knowing the different power gain definitions aids in the amplifier design process. It helps choose the right active device for the application and optimize matching networks for best amplifier performance.
📚 Resources
Microwave Engineering by David Pozar, 4th ed., chapter 12.1 has clear derivations of each of the expressions presented in this article.
Microwave Circuit Design using Linear and Nonlinear Techniques by Vendelin, Pavio and Rhode, 2nd ed., chapter 4.6 has some ADS design examples with various gain calculations. Table 4.5 is a good summary of all possible gains with their formulae.
The views, thoughts, and opinions expressed in this newsletter are solely mine; they do not reflect the views or positions of my employer or any entities I am affiliated with. The content provided is for informational purposes only and does not constitute professional or investment advice.




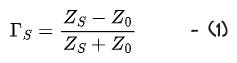









very helpful and simple explanation , thanks
Thanks Vikram for your efforts, every content is precisely explained.