How Foundries Calculate Die Yield
Understanding the metric that Intel used to abandon a whole technology node.
Intel has abandoned the 20A node to go straight to 18A.
There has been a lot of speculation on why. Some say that Intel needs all hands on deck to fix 18A because it is in trouble. Others surmise that this might actually save Intel money, and fund their 14A node.
Intel's reasoning in the statement made by Ben Sell, Intel's VP of Technology Development, is that they have already learned all they can from the 20A node, and since the 18A node is already yielding well, they can implement their learning on next node immediately.
While the business implications of this transition are of some interest to me, I have followed the coverage of this news purely as a matter of curiosity. What piqued my interest however is the key metric used by Intel to justify the switch: Defect Density.
Here is what Sell said (emphasis mine):
When we set out to build Intel 20A, we anticipated lessons learned on Intel 20A yield quality would be part of the bridge to Intel 18A. But with current Intel 18A defect density already at D0 <0.40, the economics are right for us to make the transition now.
A defect density below 0.4 means that over 67% of manufactured chips will work. As a technology goes into volume production, the defect density reported by leading fabs drops to 0.1, or over 90% yield.
In this post, we will look at how semiconductor foundries calculate defect densities and the die yields they correspond to.
Die Yield, Defects and Cleanrooms
Models for Yield Estimation
Basic and Simple: Poisson and Binomial
Based on Distribution Functions: Murphy, Seeds, Bose-Einstein
Other options suggested in literature: Moore, Negative Binomial
Comparisons of commonly used models
Read Time: 10 mins
This post is too long for email. Please read it online.
Die Yield, Defects and Cleanrooms
Semiconductor foundries, like most manufacturers, are unable to get every chip to work due to varying tolerances, faults, and physical limitations in real-world contexts. A semiconductor foundry, such as Intel, Samsung or TSMC, invests a significant amount of money and effort to boost process yields, which are often targeted to be greater than 90%. Given the huge volume of chips manufactured in foundries, die yield is a critical profitability parameter that attracts much deserved attention.
Die yield loss is related to flaws in the wafer manufacturing process. A defect is any flaw in the physical structure of a die that causes the circuit to fail. Anomalies take many forms, including shorts and opens, particle contamination, spatters, flakes, pinholes, scratches, and so on.
To reduce yield loss due to foreign particles, foundries create extremely clean environments for wafer production that are classified into different "Classes" based on the size and number of particles in one cubic foot of air.

Keep in mind that the particle count needs to be kept at such low levels for about a million square feet of factory floor area. This is made possible by large HVAC systems and high levels of HEPA filtration. To get a feeling for how clean these rooms need to be, a surgical operating theater is Class 100,000. You can imagine how impossibly difficult is to construct a Class 1 cleanroom in such large spaces. Instead, factories implement smaller trash-can sized wafer transports called Front Opening Unified Pods (FOUPs) that are Class 0.1 on the inside to move wafers different pieces of equipment inside a fab. All of this is done to decrease defect density. If you're interested, I recommend Brian Potter's "How to Build a $20 Billion Semiconductor Fab" for a fascinating journey into what it takes to build a modern semiconductor fab.
Not all yield loss is due to defects. Since deposition of materials are less controlled on the periphery of the circular wafer, manufacturing accuracy is poor, leading to edge die loss. While foundries try to minimize edge loss, it is unavoidable and such edge die are screened by parametric testing and excluded from further processing.
Defect based yield loss is a critical factor that determines the readiness of a technology for high volume manufacturing. Since the defects are random1, the die yield, symbolized as DY, is a probabilistic calculation that assumes various random defect distributions. We will look at several commonly used yield models next.
Yield Models
There is no universal model to predict the yield of a wafer based on how many defects it has in a given area. The choice of yield model depends on how the defects are distributed on the wafer (uniform, on the edges, clustered, etc.) and how big the die size is. Even these two factors are intricately linked: smaller die sizes have lower probability of defects but narrower features are more prone to having them.
Poisson and Binomial Models
The Poisson distribution, classically used to describe radioactive decay, describes the probability that k defects can simultaneously occur in a die if the mean number of defects in a die is λ0, and is given by
Let's say that D0 is the defects per square centimeter and A is the die area in square centimeters so that λ0 = D0⨉A. For a die to work, we need zero defects. Die yield DY is therefore P(k=0), and is a simple exponential function.
Assuming a 1 square centimeter chip, and a defect density of D0=0.4/cm2, the die yield is 67%. For D0=0.1, the die yield is 90%. If a wafer fab measures the die yield from a wafer, they can calculate the defect density by
Poisson's yield model usually works well for the die sizes are small compared to the wafer diameter and when the defects are quite uniformly distributed along the wafer.
A variation of the Poisson model, but more generalized for area is called the Binomial model. Instead of using mean defects per area for calculation, it uses the total number of defects on the wafer, and calculates the probability that a defect will be present on any given die assuming a Binomial distribution. If the wafer area is much bigger than die area, which it usually is in a 12" silicon wafer, then it reduces to the Poisson model. We will not get into it too much because the Poisson model is more widely used anyway.
Murphy, Seeds and Bose-Einstein Models
Poisson and Binomial models assume that defects are randomly distributed across the wafer. In many cases, defects tend to cluster around each other and once a defect occurs on a chip, it is excluded and other defects on it are irrelevant. For larger die sizes, more defects can cluster on the same chip and in such cases, the Poisson model tends to underestimate the yield of the chip.
To make it more general, the defect density (D) can be expressed as a distribution f(D), with a mean value of D0. Based on this B. T. Murphy of Bell Labs proposed die yield calculation as
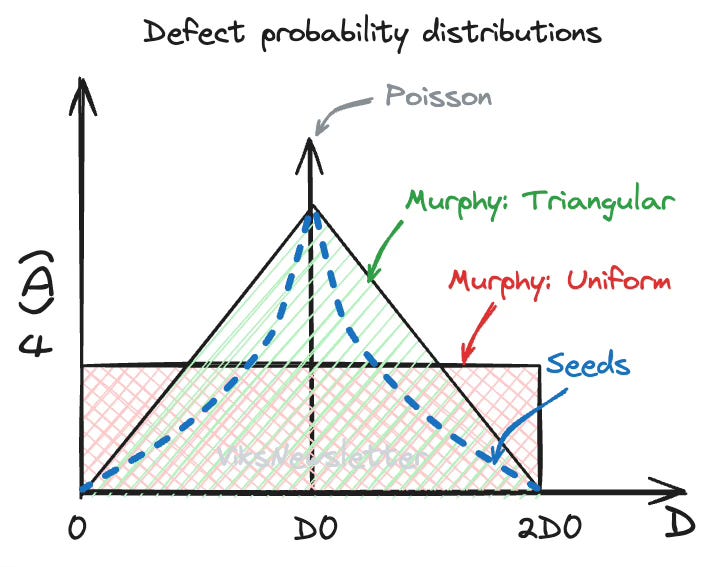
The figure below shows a few forms that f(D) can take depending on how defects are distributed on the wafer.
If f(D) is a delta-function with mean D0, calculation of die yield will result in the Poisson estimation.
If f(D) is uniformly distributed between 0 and 2D0, die yield after integration is given by
If f(D) approximates a Gaussian distribution with a triangular function, die yield after integration is given by
The triangular distribution and resulting die yield is called the Murphy Model.
If f(D) takes on an exponential distribution, the die yield after integration will result in
This is known as the Seeds Model.
An extension of the Seeds model is the Bose-Einstein model which takes into account that 'n' critical layers in the processing of a wafer could each have its own defect density. The die yield calculation for the Bose-Einstein model is given by (where DD is the defect density per layer)
A slight difference is the calculation of the Bose-Einstein defect model comes from what defect density means in this case. In all the other calculations involving D0, the units are defects per square-centimeter. But most foundries report DD used in the Bose-Einstein model in defects per layer per square inch. You can convert between the D0 and DD using an online calculator, or using my free google sheets calculator.
Another caveat is, by no means do defect densities have to be the same in every critical manufacturing layer in the calculation of Bose-Einstein yield. If they are different, the die yield for each layer can be multiplied instead of calculating the power of ‘n’.
Other Models
For large die sizes and a more flexible model for yield, f(D) can be chosen to be a Gamma distribution that results in a yield model called Negative Binomial Model whose die yield can be expressed as
This equation requires an estimated value for 𝛼 called the cluster parameter, which depends on the mean and standard deviation of defects on the die. Depending on the value of 𝛼, the negative binomial model can be made to emulate other models such as Poisson (𝛼>10), Murphy (𝛼=5), and Seeds (𝛼=1) models.
In 1970, Gorden Moore proposed a yield model in a paper titled “What level of LSI is best for you?” that is a slight variation on the Poisson model, and is used occasionally.
Putting it all together
The plots below show the die yields calculated using the most popular yield models. As long as the die size is relatively small, the Poisson model is the most commonly used due to its simplicity. For larger die sizes, the Murphy model with triangular distribution or the Bose-Einstein model is most commonly used. Regardless of the yield model used (except Bose-Einstein), the die yield for D0=0.4 defects/cm2 is about 67-71%.
Foundries report defect density DD in units of defects/inch2/layer for Bose-Einstein model calculations. The results also depend on the number of critical layers in the process. Smaller the technology node, the higher the number of critical layers, and the harder it is to get good yields. The plot below shows a criticality factor of 35.5 which is representative for a 5nm node.
Regardless of the calculation method used, a defect density of D0 < 0.1 defects/cm2 results in a die yield of about 90%, which indicates a mature, manufacturable technology node.
More Resources
Access my Google Sheet used to calculate all die yield models in this article here.
Online calculator to estimate the number of dies per wafer given a defect density that uses Murphy's Model for yield calculations.
Yield Modeling and Analysis by Prof. Robert C. Leachman
B. T. Murphy, “Cost-size optima of monolithic integrated circuits,” Proc. IEEE, vol. 52, no. 12, pp. 1537–1545, 1964, doi: 10.1109/PROC.1964.3442.
I. Tirkel, “Yield Learning Curve Models in Semiconductor Manufacturing,” IEEE Trans. Semicond. Manufact., vol. 26, no. 4, pp. 564–571, Nov. 2013, doi: 10.1109/TSM.2013.2272017.
N. Kumar, K. Kennedy, K. Gildersleeve, R. Abelson, C. M. Mastrangelo, and D. C. Montgomery, “A review of yield modelling techniques for semiconductor manufacturing,” International Journal of Production Research, vol. 44, no. 23, pp. 5019–5036, Dec. 2006, doi: 10.1080/00207540600596874.
J. E. Price, “A new look at yield of integrated circuits,” Proc. IEEE, vol. 58, no. 8, pp. 1290–1291, 1970, doi: 10.1109/PROC.1970.7911.
If you like this post, please click ❤️ on Substack, subscribe to the publication, and tell someone if you like it. 🙏🏽
If you enjoyed this issue, reply to the email and let me know your thoughts, or leave a comment on this post.
We have a community of RF professionals, enthusiasts and students in our Discord server where we chat all things RF. Join us!
The views, thoughts, and opinions expressed in this newsletter are solely mine; they do not reflect the views or positions of my employer or any entities I am affiliated with. The content provided is for informational purposes only and does not constitute professional or investment advice.
They could be systematic too, and the way to look at that is different from pure probabilistic calculations.


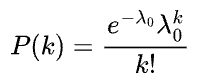










I used to live this stuff as a foundry manager (TSMC). My employer, an IDM, was horrified to learn that I tracked make-vs-buy options for my internal product group customers. Lots of head-in-the-sand behavior. 😳
Given that Intel's chip is bigger in die size, should not the actual yield rate be lower for the same defect density?